Biophysical basics in Biology and Medicine

Over the last 70 years, there have been major changes in the understanding of biological development, the handling of complex systems, non-linear mathematical functions and material self-organisation in physics. These changes in scientific concepts, which can be described as paradigm changes, have not yet really arrived in medicine. This was difficult if only because in the 1950s the “genetic programme” of Jacob and Monod((F. Jacob: Die Logik des Lebenden. From primordial generation to the genetic code. 1972) , a recapitulation of the old preformation theory found acceptance. However, this was in contrast to the simultaneously developed concepts of self-organisation of order in non-equilibrium thermodynamics (I. Prigogine, 1950), complexity science in non-linear functions (B.B. Mandelbrot, 1977), epigenesis (C.H.Waddington, 1944), the mathematical description of morphogenesis (D’Arcy Thompson 1917, A Turing, 1952). Since today’s active physicians usually limited their scientific school subjects to biology (better grade point average for the NC), they only learnt the reductionist molecular biology taught at this time. The entire organism has disappeared from biology (B. Goodwin). This has changed, for example, with the surprising results of the Human Genome Project at the beginning of this century, but too late for the currently still prevailing doctrines, which propose a molecular psychiatry and thus miss an understanding of chronic diseases as a system with a stable attractor. This may explain the complete failure of medicine to understand chronic diseases and the lack of causal therapies. Mechanistic models such as the leakage model of barrier function can also be attributed to this. The immunological network that could explain many of the phenomena associated with immune system associated pathologies is still missing from the curricula. I have pointed out these connections in a book with corresponding references (CSF diagnostics in neurology. Paradigm change in brain barriers, immune system and chronic diseases. Springer 2024. ISBN 978-3-662-68839-7

The following two scientific topics seem to be of particular  relevance to me:

I. Material self-organization in Physics, Chemistry and Biology. Emergence of order as consequence of nonequilibrium Thermodynamics

Order

When energy is supplied, order is created in physical, chemical, biochemical and biological systems.
The simplest example is the convection of water molecules in slowly heated water (Bénard figures in Fig.). As the temperature gradient increases, clusters of coherent movement of the water molecules (convection, flow) arise spontaneously. Turbulence occurs, dividing the liquid into cells. We obtain diffusion-convection interfaces. If the temperature is increased further, the great disorder suddenly and spontaneously becomes a new state of order, without any new organizing force having acted (see Bénard figures below).
A turbulent system has order insofar as the movements of two molecules, between which there is a macroscopic distance (to be measured in centimetres), are nevertheless correlated. In contrast, a crystal with its incoherent atoms oscillating around the equilibrium position is disordered in terms of its thermal movement. In this sense, far from thermodynamic equilibrium, turbulence is more likely than disorder. In equilibrium, the particles (e.g. atoms in a gas) are only weakly correlated, whereas the correlation range in non-equilibrium (correlation in turbulence etc.) is up to 108 times greater.
Order is understood here as coherent molecular movements.
These processes are characteristic for non-equilibrium thermodynamics.

Abb: Bénard figures in a thin layer of water with slow heating. The liquid is mixed with aluminium particles for better visibility

Non-equilibrium thermodynamics

The chemical reaction that leads to chemical equilibrium, producing heat and entropy, is a well-known example from Boltzmann’s classical equilibrium thermodynamics. The nonequilibrium Thermodynamics are a crucial extension of the classic view of the 2^nd law of Thermodynamics for which Ilya Prigogine won the Nobel Prize. Prigogine argued that as long as systems receive energy and matter from an external source, nonlinear systems (or dissipative structures, as he called them) can go through periods of instability and then self-organization, resulting in more-complex systems. The emergence of order as a process far from equilibrium is accompanied by the generation of negative entropy, negentropy. This is a characteristic of all living systems (E. Schrödinger). Prigogine’s work dealt with the application of the 2nd Law of thermodynamics to complex systems, including living organisms.

References

Reiber H. (2024) Cerebrospinal fluid diagnostic in Neurology. Paradigm change in brain barriers, immune system and chronic diseases. Springer 2024. ISBN 978-3-662-68839-7
G. Nicolis, I. Prigogine: Self-Organization in Nonequilibrium Systems. Wiley-Interscience, NY, 1977, ISBN 0-471-02401-5.
Ilya Prigogine: Die Gesetze des Chaos. Insel, Frankfurt 1998, ISBN 3-458-33885-3.
Schröder M (1994) Fraktale, Chaos und Selbstähnlichkeit, Spektrum-Verlag, Heidelberg.
Haken H. Synergetics.Nonequilibrium-Phase transitions in Physics, Chemistry and Biology. Springer, Berlin, 3rd ed.1983
Schrödinger Erwin. What is Life? 1944 with Mind and Matter and Autobiographical Sketches. Cambridge university Press, 2004, 11th Ed., (Combined from original books What is life, 1944 and Mind and Matter 1958)

II. Developmental biology: Self-organization of the phenotype as a stable attractor

Biology and Complexity

In the 1960s it was postulated that in the ontogenesis of the organism the genome steers development and that with knowledge of the genome we can also understand and cure diseases. The failure of gene therapy and also of later postulated stem cell therapy could have been anticipated from the principles of material self-organization in biological development. But only the discoveries from Drosophila genetics and the human genome project at the end of the last century have fundamentally changed genetics and the concept of the gene. Concepts such as alternative splicing in gene expression or RNA interference, the post-transcriptional control of mRNA by micro-dsRNA, as well as gene silencing, the switching off of unused genes by methylation, have given rise to a new view on epigenesis in development.
Genome and Phenotype
Whatever can be expressed from a genome, it only takes shape if it is associated with a process that has a stable form, i.e. an attractor. Brian Goodwin (1997) has shown this excellently with the self-organised, calcium-dependent development of the phylotypic form, the leaf formation, in the algae Acetabularia.
Stability of the functioning organism is not guaranteed by the genome, which is subject to constant mutations. Genexpression itself is a phenotype based selforganization process. Only the material realisation as a phenotype has stability criteria.
Every new mutation in the genome is subject to this reality check, i.e. phenotypic realisability. Richard Dawkins had not considered this in his idea of the ‘selfish gene’.
The rationality of an organism’s development comes from the emergence of order and form through the self-organisation of matter. At this point with are confronted also with a new understanding of Epigenesis.

Non-linear functions determine biology

Every feedback as a prerequisite for biochemical metabolic control in biology leads to a quadratic term of the corresponding function and thus represents a non-linear function. This is the basis of the deterministic-chaotic time series which can be measured. The interpretation of these empirically determined time series require the methods of complex systems. These are mainly the formation of a graphical return plot and the calculation of the  Complexity by a fractal dimension (Power law).

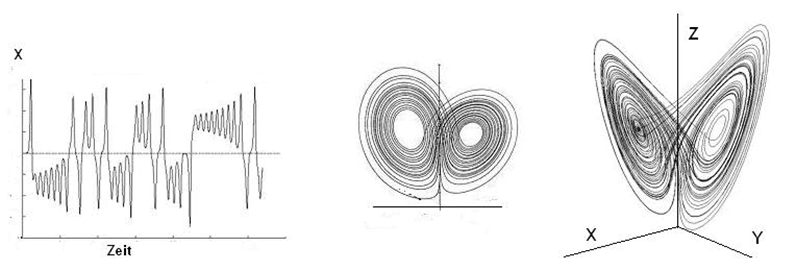
Fig. The figure shows the path from the time series (left) to the reconstructed phase portrait (return plot) with 2 (centre) and 3 dimensions (right) (referred to as embedding dimensions). The lines represent the successive states calculated by iteration for a Lorenz attractor, called trajectories.

Fractal dimensions determine our world

There is no straight line (D=1), plane surface (D=2) or purely three-dimensional spatial form (D=3) in nature. We find so-called fractal dimensions (D= 1.7; 2.4; but also D= 7.3).
The fractal dimension is an expression of the complexity of a function and can be determined empirically. This can be used in the double logarithmic plot to represent changes in complexity (e.g. disease) or to recognize them in the first place.

Biological stability is defined by the attractor

Regardless of the type and extent of deflection, the pendulum always returns to the lowest point of the oscillation path due to gravity (point attractor). Similarly, “biologically stable” (steady state, etc.) systems find a state that can be represented with the typical state space of the system, e.g. developed from an empirical time series in the return plot (phase portrait in Fig.). Systems without attractors are not found in the evolution of organisms or in developmental biology. That is also the case for chronic diseases.

Methodical applications in medicine

From glycolysis oscillation, changes in heart rate or osteoporosis to changes in alpha waves in the electroencephalogram of the brain during epileptic seizures, the methods of complex systems have gained practical relevance. Correspondingly, without knowledge of complex systems, it is impossible to understand the development of chronic diseases or to develop a suitable causal therapy. A chronic disease is to be treated under the following aspects

1. Chronic disease is a stable state, i.e. the corresponding regulation has an attractor
2. Pathological regulation change can be characterized by a lower complexity. This may be associated with lower biological stability.
   These aspects are the basis of new diagnostics and therapeutic concepts for chronic diseases.

References

Reiber H (2007) Die Komplexität biologischer Gestalt als zeitunabhängiges Konstrukt im Zustands-Raum. Zum naturwissenschaftlichen Umgang mit Qualitäten. In: Doris Zeilinger (Hg): VorSchein, Jahrbuch der Ernst-Bloch- Assoziation, Antogo Verl. Nürnberg, S. 39-61
Reiber H (2012). Komplexität und Selbstorganisation stabiler biologischer Gestalt in Epigenese und Evolution –Von der genozentrischen zur phänozentrischen Biologie. In: Kaasch, et al (Hrsg.). Verhandlungen zur Geschichte und Theorie der Biologie, Berlin: VWB. Bd. 17, S. 37 – 80
Reiber H (2012). Epigenesis and epigenetics- understanding chronic diseases as a selforganizing stable phenotype Neurol. Psych. Brain Res. 18: 79-81
Reiber H, Davey B (1996). Desert-storm-syndrome and immunization. Arch Internal Med 156:217.
Goodwin BC (2007). How the Leopard Changed Its Spots: The Evolution of Complexity. NJ: Princeton University Press. und (1997) Der Leopard, der seine Flecken verliert. Evolution und Komplexität. Piper Verlag, München.
Thompson, D’Arcy W (1917). On Growth and Form. (Ed. by J. T. Bonner); Cambridge Univ. Press, Canto Classics 3rd printing
Turing, A. M. (1952) The chemical basis of morphogenesis. Phil. Trans. R. Soc. B. 237, 37–72
Briggs J, Peat F D (1997). Die Entdeckung des Chaos. DTV, München
Gleick J (1987). Chaos. Making a New Science. Penguin Books, N.Y.
Ilya Prigogine: Die Gesetze des Chaos. Insel, Frankfurt 1998, ISBN 3-458-33885-3
Schröder M (1994) Fraktale, Chaos und Selbstähnlichkeit, Spektrum-Verlag, Heidelberg.
Hess B, Boiteux A (1980). Glykolyse Oszillation. Ber. Bunsenges.Phys. Chem. 84:392
MANDELBROT BB (1977). Fractals: Form, Chance and Dimension. WH Freeman &Co